Page 44 - 今日电机

差均较小；kb过大时，不仅q轴磁路饱和，d
轴磁路饱和程度也大大增加，同样导致较低的输
出转矩和功率因数。图10为不同磁障占比下输出
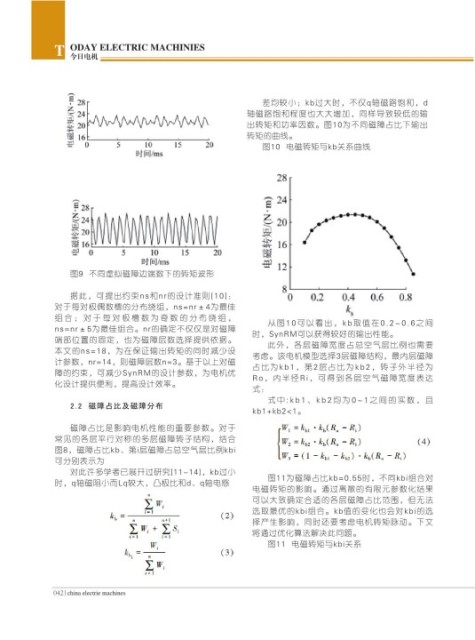
转矩的曲线。
图10 电磁转矩与kb关系曲线

图9 不同虚拟磁障边端数下的转矩波形

据此，可提出约束ns和nr的设计准则[10]：
对于每对极偶数槽的分布绕组，ns=nr±4为最佳
组合；对于每对极槽数为奇数的分布绕组， 从图10可以看出，kb取值在0. 2~0. 6之间
ns=nr±5为最佳组合。nr的确定不仅仅是对磁障 时，SynRM可以获得较好的输出性能。
端部位置的固定，也为磁障层数选择提供依据。
此外，各层磁障宽度占总空气层比例也需要
本文的ns=18，为在保证输出转矩的同时减少设 考虑。该电机模型选择3层磁障结构，最内层磁障
计参数，nr=14，则磁障层数n=3。基于以上对磁 占比为kb1，第2层占比为kb2，转子外半径为
障的约束，可减少SynRM的设计参数，为电机优 Ro，内半径Ri，可得到各层空气磁障宽度表达
化设计提供便利，提高设计效率。
式：
式中: kb1、kb2均为0~1之间的实数，且
̻̿̿ḤḤՈᅰᅝбࠣՈᅰٳ҃
kb1+kb2<1。
磁障占比是影响电机性能的重要参数。对于
常见的各层平行对称的多层磁障转子结构，结合
图8，磁障占比kb、第i层磁障占总空气层比例kbi
可分别表示为
对此许多学者已展开过研究[11-14]，kb过小
时，q轴磁阻小而Lq较大，凸极比和d、q轴电感 图11为磁障占比kb=0.55时，不同kbi组合对
电磁转矩的影响。通过离散的有限元参数化结果
可以大致确定合适的各层磁障占比范围，但无法
选取最优的kbi组合。kb值的变化也会对kbi的选
择产生影响，同时还要考虑电机转矩脉动。下文
将通过优化算法解决此问题。
图11 电磁转矩与kbi关系
图12 转矩与磁肋宽度关系

china electrie machines